Control Structures - Conditional Execution

• The LOGICAL type
• Logical expressions
  • Relational expressions
  • Composite logical expressions
• Logical assignment
• The logical IF statement
• The block IF structure

The FORTRAN statements covered so far are enough to allow us to read information, evaluate arithmetic expressions and print results. It is hardly necessary to write a program to perform such tasks, which can usually be more easily done using a calculator.

The main advantages of a computer are its ability to:

• execute alternative sequences of instructions depending on a condition (conditional execution).
• execute a sequence of instructions repeatedly while or until a condition is satisfied (iteration).

This chapter deals with conditional execution while iteration is covered in Chapter 6.

The need for conditional execution is illustrated by the following problem:

Example 1:

Write a program to read the coefficients of a quadratic equation and print its roots.

Solution: The roots of the quadratic equation

are given by the formula

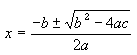
The outline of the program is:

1. Read the coefficients.
2. Evaluate .
3. If exceeds zero then
   1. Compute and print two distinct real roots.

Otherwise, if is equal to zero then

1. Compute and print two coincident real roots.

Otherwise

1. Print message: 'No real roots.'

In step 3, the program must test conditions such as ' exceeds zero'. To express such conditions, FORTRAN uses another type, the LOGICAL type.

The LOGICAL type

There are two LOGICAL constants, defined as .TRUE. and .FALSE..

A LOGICAL variable can be assigned either of these values. It may not be assigned a value of any other type. Each LOGICAL variable must be declared in a LOGICAL type specification statement, which must occur, like all other type specifications, before the first executable statement.

Example:

The LOGICAL variable ERROR could be declared and initialised by the statements:

	LOGICAL ERROR
	ERROR = .FALSE.

Logical expressions

A logical expresssion is one which evaluates to one of the LOGICAL constants .TRUE. or .FALSE.. Thus the simplest logical expressions are the LOGICAL constants themselves, and LOGICAL variables.

Relational expressions

A relational expression is a logical expression which states a relationship between two expressions, evaluating to .TRUE. if the relationship applies or .FALSE. otherwise. For the present, we shall consider only relationships between arithmetic expressions. (As we shall see later, FORTRAN can also deal with relationships between CHARACTER expressions.)

A relational expression has the form:

arithmetic_expression relational_operator arithmetic_expression

The relational operators are:

       Meaning               

.LT.   Less than             

.LE.   Less than or equal    
       to                    

.EQ.   Equal to              

.NE.   Not equal to          

.GE.   Greater than or       
       equal to              

.GT.   Greater than          

Thus examples of relational expressions are:

	N.GE.0
	X.LT.Y
	B**2 - 4*A*C .GT. 0.

Notes:

1. Relational operators have lower precedence than arithmetic operators. Therefore, in evaluating a relational expression, the arithmetic expressions are evaluated before the comparison indicated by the relational operator is made.
2. The two arithmetic expressions may be of different type (i.e. one INTEGER and one REAL). In this case, the INTEGER expression is converted to REAL form before the comparison is made.

Composite logical expressions

It is often necessary to express a condition which combines two or more logical expressions. For example, to check that the value of a variable lies within a given range, we should have to check that it is greater than the lower limit AND less than the upper limit. Such conditions are expressed in FORTRAN by composite logical expressions, which have the form:

L1 logical_operator L2

where L1 and L2 are logical expressions (relational or composite). The logical operators and their meanings are shown below. The second column indicates the conditions under which a composite logical expression as above evaluates to .TRUE..

         Meaning                                              

.AND.    Both L1 and L2 are .TRUE.                            

.OR.     Either L1 or L2 or both are .TRUE.                   

.EQV.    Both L1 and L2 have the same value (.TRUE. or        
         .FALSE.)                                             

.NEQV.   L1 and L2 have different values (one .TRUE. and one  
         .FALSE.)                                             

Thus the following composite logical expression would evaluate to .TRUE if the value of the variable X lay within a range with non-inclusive limits MIN and MAX.:

	X.GT.MIN .AND. X.LT.MAX

There is one further logical operator .NOT., which unlike the others, takes only one operand, which it precedes. The expression .NOT.L is .TRUE. if the logical expression L is .FALSE. and vice versa.

As with arithmetic operators, precedence rules are required to define the interpretation of expressions like:

.NOT. L1 .OR. L2

which could evaluate to .TRUE. under either of the following conditions, depending on the order of evaluation:

1. L1 is .FALSE. or L2 is .TRUE.
2. L1 and L2 are both .FALSE.

The precedence order is shown by the following list, in which precedence decreases downwards.

arithmetic operators

relational operators

.NOT.

.AND.

.OR.

.EQV. and .NEQV.

Thus (i) is the correct interpretation of the above expression.

As in arithmetic expressions, parentheses can be used to group partial logical expressions and change the order of evaluation. Thus

.NOT.(L1.OR.L2)

would be evaluated according to interpretation (ii).

Parentheses can also be used to improve clarity, even when not logically required, e.g.

(A.LT.B) .OR. (C.LT.D)

Logical assignment

The value of a logical expression can be assigned to a variable of type LOGICAL, e.g.

	LOGICAL VALID
		...
	VALID = X.GT.MIN .AND. X.LT.MAX

Logical expressions are more commonly used in logical IF statements and structures.

The logical IF statement

The logical IF statement is used to execute an instruction conditionally. It has the form:

IF (logical_expression) executable_statement

where executable_statement is an executable FORTRAN statement other than another IF statement or a DO statement (see Chapter 6).

The statement is executed by evaluating logical_expression and executing executable_statement if it evaluates to .TRUE..

Example: IF (A.LT.B) SUM = SUM + A

The block IF structure

The logical IF statement is of limited usefulness, as it permits only the execution of a single instruction depending on a single condition. The block IF structure is more powerful, permitting the conditional execution of one of a number of alternative sequences of instructions. It may be described informally as:

• an IF block, followed by:

• one or more optional ELSE IF blocks, followed by:
• an optional ELSE block, followed by:
  • END IF

More formally, the structure is:

IF () THEN

ELSE IF () THEN

...

ELSE

END IF

where:

• and are logical expressions.
• , and are sequences of FORTRAN statements.
• The square brackets ( [] ) indicate that an item is optional and the ellipsis (...) that it may be repeated indefinitely.

The structure is executed as follows:

is evaluated. If it evaluates to .TRUE., the sequence is executed and execution continues with the statement following END IF.

Otherwise:

1. If there are any ELSE IF clauses, each is evaluated, until either:
   1. An evaluates to .TRUE.. The sequence is executed and execution continues with the statement following END IF.

or:

1. The last evaluates to .FALSE.. Execution continues with step 2.

1. If there is an ELSE clause, the sequence is executed.
2. Execution continues with the statement following END IF.

Thus, a simple block IF structure is:

	IF (A.LT.B) THEN
	SUM = SUM + A
	PRINT *, SUM
	END IF

which is equivalent to the IF statement shown earlier.

A more realistic example is the following:

Example:

An employee is paid at the standard rate for the first 40 hours of work, at time and a half for the next 10, and at double time for any hours in excess of 50. If the variable HRS represents the hours worked and RATE the standard rate then the employee's salary is computed by the block IF structure:

	IF (HRS.LE.40) THEN
		SALARY = HRS*RATE
	ELSE IF (HRS.LE.50) THEN
		SALARY = 40.0*RATE + (HRS-40.0)*RATE*1.5
	ELSE
		SALARY = 40.0*RATE + 10.0*RATE*1.5 + (HRS-50.0)*RATE*2.0
	END IF

Note the use of indentation to clarify the structure.

We are now in a position to complete the quadratic roots program of Example 1, but first the outline should be altered as follows:

1. Because REAL values are approximations, exact comparisons involving them are unreliable. The relational expressions in our program should therefore be reformulated using a variable (for error) to which a small positive value has previously been assigned. The expression ' exceeds zero' in step 3 should be replaced by:

>

Similarly, the expression ' is equal to zero' in step 3 should be replaced by:

However, the expression is evaluated only if > has previously been evaluated as false, which of course implies . Therefore, all that is required is:

Comparisons involving REAL values should always be expressed in this way.

1. The expression for the roots includes a divisor of . Therefore if has a value of zero, the evaluation of this expression will cause the program to fail with an arithmetic error. The program should prevent this by testing and printing a suitable message if it is zero. Again, the test should be expressed using the error variable .

In general, programs should be designed to be robust, i.e. they should take account of any exceptional data values which may cause the program to fail, and take steps to prevent this.

The program outline now becomes:

1. Assign a small positive value to .

1. Read the coefficients.
2. If then
   1. Print message: 'First coefficient must be non-zero'.

Otherwise:

1. Evaluate
2. If > then
   1. Compute and print two distinct real roots.

Otherwise, if then

1. Compute and print two coincident real roots.

Otherwise

1. Print message: 'No real roots.'

Now that the outline is complete, the program can be easily written:

	PROGRAM QUAD
	E = 1E-9
	READ *, A,B,C
	IF (A.GE. -E .AND. A.LE.E) THEN
	PRINT *, 'FIRST COEFFICIENT MUST BE NON-ZERO.'
	ELSE
	S = B**2 - 4*A*C
	IF (S.GT.E) THEN
	D = S**0.5
	X1 = (-B+D)/(2*A)
	X2 = (-B-D)/(2*A)
	PRINT *, 'TWO DISTINCT ROOTS:' X1 'AND' X2
	ELSE IF (S.GT. -E) THEN
	X = -B/(2*A)
	PRINT *, 'TWO COINCIDENT ROOTS',X
	ELSE
	PRINT *, 'NO REAL ROOTS.'
	END IF
	END IF
	END

Figure 7: Quadratic roots program

Note that most of the program consists of a block IF structure, with a second block IF included in its ELSE clause. The embedding of one structure within another in this way is called nesting.

Once again, indentation has been used to clarify the structure.

[Contents]  [Previous]  [Next]  [Home]

NDP77
http://www.ndp77.net
webmaster Massimo F. ARENA
webmaster@ndp77.net
2004:02:14:17:30:17